The fundamental nature of quantum gravity remains one of the most challenging problems in theoretical physics. Recent work by Oscar J. C. Dias from the University of Southampton and Jorge E. Santos from the University of Cambridge, along with their colleagues, explores potential solutions using a framework known as Banks-Fischler-Shenker-Susskind (BFSS) matrix mechanics. Their research investigates the unusual localized states that emerge within this system, providing a detailed analysis of their properties.
Their findings demonstrate that these strongly coupled dynamics arise from a specific transformation of eleven-dimensional supergravity, revealing a surprising connection between matrix mechanics and established gravitational theories. Crucially, the team identifies an instability within the uniform phase of BFSS, leading to the formation of localized states that dominate at low energies and temperatures. They accurately characterize the transitions between these phases with unprecedented precision.
Unveiling the Connection: BFSS Matrix Model and Gravity
Building upon the established framework of the Banks-Fischler-Shenker-Susskind (BFSS) matrix quantum mechanics, this work provides first-principles derivations of its properties and extends existing results with new analytical and numerical insights. The research demonstrates that strongly coupled BFSS dynamics emerge from a specific Carrollian transformation of 11-dimensional supergravity, a connection rigorously justified within the study.
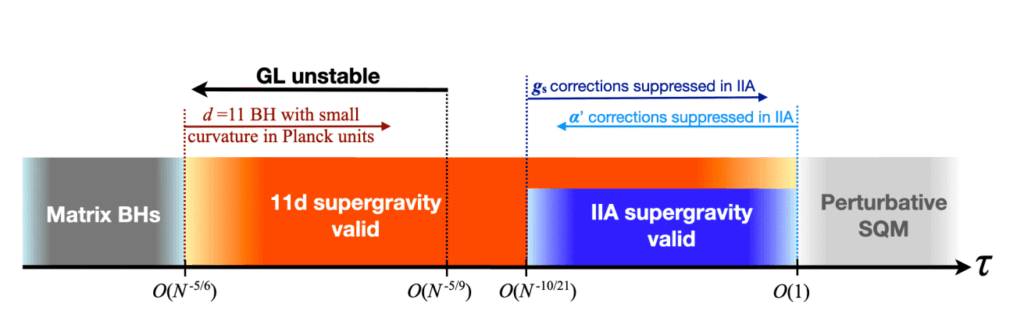
This framework establishes a correspondence between the uniform BFSS phase and a black string in a wave-like background. Importantly, the research demonstrates that this background is unstable to a Gregory-Laflamme instability. For the first time, the associated growth rate has been computed, revealing critical information about the system’s behavior. The resulting instability gives rise to non-uniform and localized phases that dominate the microcanonical ensemble in certain low-energy regimes, providing a comprehensive understanding of the system’s phase diagram.
Black Holes, Gauge Theory, and Holography
This extensive bibliography covers a broad range of theoretical physics, particularly related to black holes, string theory, gauge theory, and the holographic principle. The collection focuses on black hole physics, exploring solutions in various dimensions, their stability, phase transitions, and the information paradox.
A significant portion of the references relates to the AdS/CFT correspondence, which proposes a duality between gravitational theories in Anti-de Sitter space and conformal field theories on its boundary. This allows researchers to study strongly coupled systems using classical gravity. Many papers explore the application of AdS/CFT to understand strongly coupled gauge theories, particularly N=4 Super Yang-Mills, including their thermal properties, phase transitions, and real-time dynamics.
The study of black holes, gauge/gravity duality, and the information paradox is a very active area of research, drawing on concepts from general relativity, quantum field theory, string theory, quantum information theory, and numerical methods.
The black hole information paradox continues to be a central problem, driving much of the research in this area. Entanglement entropy plays a crucial role in understanding the information paradox and the holographic principle, and several references highlight concepts like entanglement wedge reconstruction.
BFSS Matrix Model Links Gravity and Instability
Scientists are advancing our understanding of the fundamental connection between gravity and quantum mechanics through detailed analysis of the Banks-Fischler-Shenker-Susskind (BFSS) matrix model, a theoretical framework linking quantum mechanics to gravity. This work provides first-principles derivations of the model’s properties, extending previous results with new analytical and numerical insights.
Researchers demonstrate that strongly coupled BFSS dynamics emerge from a specific transformation of 11-dimensional supergravity, rigorously justifying this connection. Within this framework, the uniform BFSS phase corresponds to a black string existing within a wave-like background.
Experiments reveal that this background is unstable to a Gregory-Laflamme instability, a phenomenon where small perturbations grow exponentially. Scientists have, for the first time, computed the associated growth rate, measuring it precisely. This instability leads to the formation of non-uniform and localized phases, which dominate the system’s behavior at low energies, with the localized phase also prevailing at low temperatures in the canonical ensemble.
Black String Instability and Phase Transitions
This research presents a detailed analysis of the behavior of strongly coupled systems described by Banks-Fischler-Shenker-Susskind (BFSS) matrix mechanics. The team successfully demonstrated that these dynamics can emerge from a specific transformation applied to eleven-dimensional supergravity, establishing a clear connection between these theoretical frameworks.
Importantly, the study identified and characterized different phases of this system, including a uniform phase corresponding to a black string in a particular background, and localized, non-uniform phases. The research revealed that the uniform black string is unstable, undergoing a Gregory-Laflamme instability that leads to the formation of these localized phases.
Through analytical calculations and numerical simulations, the team accurately determined the growth rate of this instability and mapped out the conditions under which the localized phase dominates, both in the microcanonical and canonical ensembles at low energies. The findings include precise formulas for the entropy of the localized phase, validated by comparison with numerical results.
The study of these phenomena not only provides deeper insights into the behavior of quantum gravity but also enhances our understanding of the fundamental principles that govern the universe. As researchers continue to explore these complex interactions, the potential for new discoveries in theoretical physics remains vast.






